Sign up to mark as complete
Sign up to bookmark this question
Bankrupt
Two players, A and B, play a game in which the winner receives 1 dollar from the other player. Player A has 1 dollar and player B has 2 dollars. Player A is better in this game and wins 2/3 of the games. They play until one of them is bankrupt.
What is the probability that player A wins?
What is the probability that player A wins?
Hint
Take a look at the lesson on Markov Chain Probability
Solution
This is a pretty straightforward Markov chain problem. There are 4 states. The transition graph is given in Figure 1.
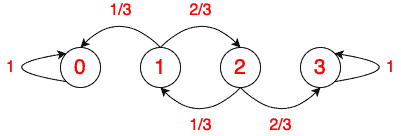
Figure 1 - Transition graph for this problem.
The problem starts at state 1. As has been explained in the lessons of this course, we use the following equation:
\begin{equation}
s_1 = \sum_{i=0}^{3}p_{1,i}s_i
\end{equation} \begin{equation}
s_2 = \sum_{i=0}^{3}p_{2,i}s_i
\end{equation} Furthermore, $s_0=0$ and $s_3=1$. Then we have
\begin{equation}
s_1 = \frac{1}{3}*0 + \frac{2}{3} * s_2
\end{equation} \begin{equation}
s_2 = \frac{1}{3}* s_1 + \frac{2}{3} * 1
\end{equation} Solving these equations gives us $s_1=4/7$ and $s_2=6/7$. So, starting with 1 dollar, player A has a 4/7 chance of winning.
Proof
If we substitute Equation 4 in Equation 3, we have
\begin{equation}
s_1 = \frac{1}{3}*0 + \frac{2}{3} * (\frac{1}{3}* s_1 + \frac{2}{3} * 1)
\end{equation} \begin{equation}
s_1 = \frac{2}{9} * s_1 + \frac{4}{9}
\end{equation} \begin{equation}
\frac{7}{9} * s_1 = \frac{4}{9}
\end{equation} \begin{equation}
s_1 = \frac{4}{9} / \frac{7}{9} = \frac{4}{7}
\end{equation}
The problem starts at state 1. As has been explained in the lessons of this course, we use the following equation:
\begin{equation}
s_1 = \sum_{i=0}^{3}p_{1,i}s_i
\end{equation} \begin{equation}
s_2 = \sum_{i=0}^{3}p_{2,i}s_i
\end{equation} Furthermore, $s_0=0$ and $s_3=1$. Then we have
\begin{equation}
s_1 = \frac{1}{3}*0 + \frac{2}{3} * s_2
\end{equation} \begin{equation}
s_2 = \frac{1}{3}* s_1 + \frac{2}{3} * 1
\end{equation} Solving these equations gives us $s_1=4/7$ and $s_2=6/7$. So, starting with 1 dollar, player A has a 4/7 chance of winning.
Proof
If we substitute Equation 4 in Equation 3, we have
\begin{equation}
s_1 = \frac{1}{3}*0 + \frac{2}{3} * (\frac{1}{3}* s_1 + \frac{2}{3} * 1)
\end{equation} \begin{equation}
s_1 = \frac{2}{9} * s_1 + \frac{4}{9}
\end{equation} \begin{equation}
\frac{7}{9} * s_1 = \frac{4}{9}
\end{equation} \begin{equation}
s_1 = \frac{4}{9} / \frac{7}{9} = \frac{4}{7}
\end{equation}
Related Questions
| Title | Category | Subcategory | Difficulty | Status |
|---|---|---|---|---|
| Animal Migrations | Probability and Statistics | Markov Chain Probability | Easy | |
| Bold Betting Strategy | Probability and Statistics | Markov Chain Probability | Medium | |
| Coin Series #1 | Probability and Statistics | Markov Chain Probability | Easy | |
| Coin Series #2 | Probability and Statistics | Markov Chain Probability | Medium | |
| Coin Series #3 | Probability and Statistics | Markov Chain Probability | Medium | |
| Dominant Game | Probability and Statistics | Markov Chain Probability | Hard | |
| Jumping Toad | Probability and Statistics | Markov Chain Probability | Medium | |
| Parking Meter | Probability and Statistics | Markov Chain Probability | Easy | |
| Picking Tiles | Probability and Statistics | Markov Chain Probability | Easy | |
| Random Ant | Probability and Statistics | Markov Chain Probability | Medium | Example |
| Region Spinner | Probability and Statistics | Markov Chain Probability | Easy | |
| The Drunkard's Walk | Probability and Statistics | Markov Chain Probability | Hard | |
| Top 2000 Songs | Probability and Statistics | Markov Chain Probability | Medium |
Discussion
Please log in to see the discussion.
